Respuestas a los problemas de isótopos

A continuación se pone ayuda para resolver algunos de ellos, y luego las respuestas.

Respuestas:

Asequibles, debe saberse resolverlos:
Algo más difíciles:

10,	11,	12,	13,	14,
15,	16,	17,	18,	19,
20,	21,	22,	23,	24,
25,	26,	27,	28,	29,
30,	31

Ayuda para la resolución de los problemas

Problema 10 - Ayuda

Para el cálculo de la segunda pregunta se necesita el valor de masa molecular de un nucleótido:

adenina: 135	desoxiadenosina: 251	desoxiadenílico: 331
guanina: 151	desoxiguanosina: 267	desoxiguanílico: 347
timina: 126	desoxitimidina: 242	desoxitimidílico: 322
citosina: 111	desoxicitidina: 227	desoxicitidílico: 307
		masa media de un desoxinucleótido: 327
		masa media de un nucleótido formando parte de un DNA: 327-18=309
		masa media de un par de bases: 309 x 2 = 618

Por lo tanto, una molécula de DNA de 25 Mpb tiene:
25 x 10⁶ / 618 = 40450 pb
A partir de ahí se calcula el número de timinas. Respuesta completa

Problema 12 - Ayuda

Piensa en qué otras moléculas pueden resultar marcadas. Respuesta completa

Problema 18 - Ayuda

Un proceso de desintegración radiactiva debe seguir la ecuación N = N₀ exp(-λt), o dN/dt = -λN. Se ha medido la radiactividad (cpm), que corresponde a -dN/dt, es decir, debe seguir la ecuación A = λN₀ exp(-λt).

Para obtener el valor de la constante de desintegración λ debemos ajustar los datos a esta ecuación: lo mejor es por regresión no lineal; en su defecto, tomando logaritmos: ln(A) = ln(λN₀) - λt obtenemos una recta, que se puede ajustar por mínimos cuadrados, cuya pendiente es -λ.

El tiempo de semidesintegración se relaciona con la constante de desintegración por: t_1/2 = ln2 / λ

Respuesta completa

Cálculo de actividad específica máxima (Problemas 20, 21 y 22)

La "actividad específica máxima" es la actividad específica (es decir, actividad o velocidad de desintegración, por unidad de masa o por mol) que hay cuando todos los átomos aludidos están como su isótopo radiactivo.

Por ejemplo:

Para la glucosa marcada con ¹⁴C en el C-1 ([1-¹⁴C]glucosa), cuando el átomo de C de la posición 1 sea ¹⁴C en todas las moléculas de glucosa .
Para la [¹⁴C]glucosa, cuando todos los átomos de C de todas las moléculas de glucosa sean ¹⁴C.

Respuestas completas: 20, 21, 22

Problema 23 - Ayuda

El volumen de sangre del organismo se determina a través del cálculo de la dilución.

Respuesta completa

Problema 24 - Ayuda

Si el DNA se ha marcado uniformemente, quiere decir que cualquier región de la molécula tendrá sus residuos de adenosina marcados en igual medida. Las endonucleasas producen un fragmento de la molécula, cuya composición se indica. Ésta nos indica el número de adenosinas y, por tanto, la radiactividad.

Respuesta completa

Problema 25 - Ayuda

El adjetivo "frío" se usa, en el contexto del marcaje radiactivo, para indicar el compuesto que no está marcado.

Respuesta completa

Problema 26 - Ayuda

Aplicar al proceso de mezcla los balances de masa y de radiactividad.

Respuesta completa

Problema 27 - Ayuda

a) Los signos (+) y (-) se utilizan para designar las hebras complementarias (respectivamente, hebra con sentido y hebra antisentido). En nuestro caso, basta saber que la hebra que sintetiza la DNApol es complementaria a la de partida, y por tanto tendrá A donde hubiera T, T donde hubiera A, C donde hubiera G y G donde hubiera C. La RNApol sintetizará una hebra de RNA con A donde hubiera T, U donde hubiera A, C donde hubiera G y G donde hubiera C:

DNA (+)	A	G	C	T
DNA(-)	T	C	G	A
RNA(+)	A	G	C	U

b) Se necesita la masa molecular del CTP. La citidina tiene 227, el ácido citidílico o CMP tiene 307, cada fosfato añadido supone 80 (véase la ayuda de la pregunta 10); por lo tanto, el CTP tiene 307 +80 +80 = 467.

Respuesta completa

Respuestas completas

Problema 10

a)

1 mmol equivale a 6.023·10²⁰ moléculas = 6.023·10²⁰ grupos metilo
6 Ci = 6 x 2.22·10¹² dpm
t_1/2(³H) = 12.3 años, λ = ln2 / 12.3 años
Radiactividad = –dN / dt = 6 x 2.22·10¹² dpm = ln2 / 12.3 años x 6.023·10²⁰ x f

	12.3 x 635.25 x 24 x 60 min x 6.023·10²⁰ mmol^-1
f =	––––––––––––––––––––––––––––––––––––––––––
	ln2 x 6 x 2.22·10¹² dpm/mmol

f = 0.206 es decir, el 20.6% de las moléculas son radiactivas (³H).

b)

(léase la ayuda de arriba)
Por lo tanto, una molécula de DNA de 25 Mb tiene: 25 x 10⁶ / 618 = 40450 pb
A partir de ahí se calcula el número de timinas: 40450 / 2 = 20224
(pues la mitad de los pares de bases son AT y el número de T es igual al número de pares AT).
De las cuales el 20.6% son radiactivas: 20224 x 0.206 = 4166 átomos de ³H por molécula de DNA

c)

	ln2		6.023·10²³ mol^-1 x m_DNA
Actividad = λ N =	––––––––––––––––––––––––––	x 4166 x	–––––––––––––––––––––
	12.3 x 365.25 x 24 x 60 min		25·10⁶ g/mol

luego m_DNA = 2.58·10^-13 g/min x A

	1000 cpm
A =	–––––––––––––––––	= 1923 dpm, por tanto m_DNA = 4.96·10^-10 g = 0.496 ng = 496 pg
	52 cpm / 100 dpm

Problema 11

Aquéllos cuyos espectros de emisión se solapan menos: ³H y ³²P.

Problema 12

La timidina sólo se incorpora al DNA, mientras que el fosfato se incorporará también a RNA, fosfoproteínas y fosfolípidos. Por ello, es preferible la timidina, por ser más específica, independientemente del isótopo.

Problema 13

cpm ³H }_A		cpm ¹⁴C }_A
–––––––––	= 1000	––––––––––––	= 0.2
cpm ³H }_B		cpm ¹⁴C }_B

cpm}_A = 1450
cpm}_B = 1620 suman 3070 cpm
³H en B es 0.001 = 0.1% del ³H total: despreciable (el máximo sería de 0.001 x 1450 = 1.4 cpm)
Por tanto, cpm ³H }_B » 0 , y cpm ¹⁴C }_B = 1620
cpm ¹⁴C }_A = 0.2 x 1620 = 324 y la suma cpm ¹⁴C }_A+B = 1944
cpm ³H }_A = 1450 – 324 = 1126
cpm ³H }_B = 676 / 1000 » 0 en efecto y la suma cpm ³H }_A+B = 1126
Verificamos la suma ³H + cpm ¹⁴C = 1944+1126 = 3070 correcto

Respuesta: la relación tritio/carbono-14 es de 1126/1944 = 0.58

Problema 14

a) Para una relación tritio/carbono-14 de 0.58:

0.58 cpm ³H		100 dpm ³H		82 cpm ¹⁴C		dpm ³H		Ci ³H
–––––––––––	x	–––––––––––	x	––––––––––––	= 1.90	–––––––––	= 1.90	–––––––
1 cpm ¹⁴C		25 cpm ³H		100 dpm ¹⁴C		dpm ¹⁴C		Ci ¹⁴C

	Ci ³H		mmol T		0.5 Ci ¹⁴C		mol T
1.90	–––––––	x	––––––––	x	––––––––––	= 0.158	–––––––
	Ci ¹⁴C		6 Ci ³H		mmol U		mol U

b)
Un DNA con un 43% de G+C tiene un (100-43)/2 = 28.5% de T. Es decir, hay 28.5 moles de T por cada 100 moles de nucleótidos.
La actividad de ³H era 1126 cpm, con lo cual:

		100 dpm		1 Ci		mmol T		100 mmol (nt DNA)
1126 cpm	x	––––––––	x	–––––––––––––	x	––––––––	x	–––––––––––––––––	=
		25 cpm		2.22·10¹² dpm		6 Ci		28.5 mmol T

= 1.19·10^-9 mmol = 1.19 pmol de desoxirribonucleótidos

Puesto que nos piden la masa de DNA, necesitamos la masa molecular media de un desoxirribonucleótido (véase la ayuda del problema 10), que es 309 y así calculamos:

1.19 pmol x 309 g/mol = 368 pg de nucleótidos = 368 pg de DNA = 0.368 ng.

En el RNA hay 28 moles de U por cada 100 moles de nucleótidos.

Similarmente, con las 1944 cpm de ¹⁴C :

		100 dpm		1 Ci		mmol U		100 mmol (nt DNA)
1944 cpm	x	––––––––	x	–––––––––––––	x	––––––––	x	–––––––––––––––––	=
		82 cpm		2.22·10¹² dpm		0.5 Ci		28 mmol T

= 7.63·10^-9 mmol = 7.63 pmol de ribonucleótidos

La masa molecular media de un ribonucleótido es de 309+16=325.

7.63 pmol x 325 g/mol = 2480 pg de nucleótidos = 2480 pg de RNA = 2.48 ng

Problema 15

	Geiger		Centelleo
muestra	señal	señal/ruido	señal	señal/ruido
75 dpm	75 x 0.22 = 16.5 cpm	16.5/6 = 2.75	75 x 0.72 = 54 cpm	54/38 = 1.42
100 dpm	100 x 0.22 = 22 cpm	22/6 = 3.67	100 x 0.72 = 72 cpm	72/38 = 1.89

A pesar de que el contador Geiger es menos eficaz (detecta menos cuentas), su relación señal/ruido es mejor, por lo que debe usarse éste.

Problema 16

	ln2		1 d		1 h
λ =	––––	= 0.0080 d^-1 x	––––	x	––––––––	= 5.5·10^-6 min^-1
	t_1/2		24 h		60 min

Problema 17

	ln2		1 d		1 h
λ =	––––	= 0.048 d^-1 x	––––	x	––––––––	= 3.3·10^-5 min^-1
	t_1/2		24 h		60 min

	N
"% inicial que queda" =	–––	x 100 = 100 x e^{-λ t}
	N_o

15 d	25 d	50 d
48.7%	30.1%	9.1%

Problema 18

(léase la ayuda de arriba)

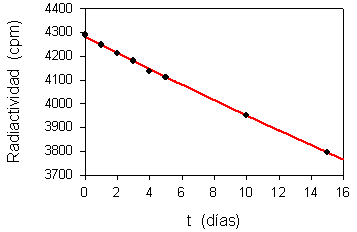
a) Representación directa de los datos y regresión no lineal:

Ecuación: Y = a exp(-bX)
a = 4281 = lN₀
b = 0.008057 = λ
r² = 0.9990
λ = 0.00806 d^-1 = 8.06·10^-3 (días)^-1
t_1/2 = ln2 / λ = 86.0 días
N₀ = 4281 / 0.00806 = 532000 = 5.32·10⁵ átomos de ³⁵S iniciales

b) Representación de los datos transformados matemáticamente y regresión lineal:

Ecuación: Y = a + b X
a = 8.362 = ln(λN₀)
b = -0.008047 = -λ
r² = 0.9991
λ = 0.00805 d^-1 = 8.05·10^-3 (días)^-1
t_1/2 = ln2 / λ = 86.1 días
N₀ = exp(8.362) / 0.00805 =531832 = 5.32·10⁵ átomos de ³⁵S iniciales

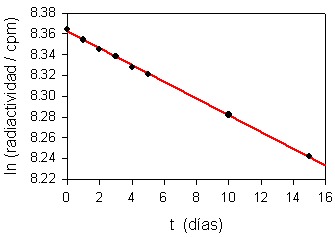(nota: aunque las gráficas parecen iguales, esto sólo es así porque los datos corresponden al inicio de la curva de desintegración; si hubiese datos a tiempos mayores se apreciaría que la de arriba es una curva exponencial y la de abajo es una recta)

Problema 19

1 Ci = 2.22·10¹² dpm; t_1/2 = 14.2 d

	ln2		ln2
λ =	––––	=	––––––––––––––––––
	t_1/2		14.2 x 24 x 60 min

–dN				ln2
––––	=	λ N	2.22·10¹² min^-1 =	––––––––––––––––––	x N
dt				14.2 x 24 x 60 min

N = 6.55·10¹⁶ átomos radiactivos
que pesan 32 u.m.a. cada uno; en total:

6.55·10¹⁶ át. x 32 g/mol
––––––––––––––––––––––	= 3.48·10^-6 g = 3.48 μg de átomos radiactivos
6.023·10²³ át./mol

(de los átomos de P no radiactivos no podemos afirmar nada, pues el dato de radiactividad no depende de ellos)

Problema 20

El periodo de semidesintegración del ¹⁴C es de 5700 años =
5700 a x 365.25 d/a x 24 h/d x 60 min/h = 3.00·10⁹ min

	ln2		ln2
λ =	––––	=	––––––––––––––	= 2.31·10^-10 min^-1
	t_1/2		3.00·10⁹ min

La actividad del ¹⁴C es:

	–dN
A =	––––	= λ N = 2.31·10^-10 min^-1 x N = N x 2.31·10^-10 dpm
	dt

		1 Ci
A =	N x 2.31·10^-10 dpm x	–––––––––––––	= N x 1.04·10^-22 Ci
		2.22·10¹² dpm

La glucosa tiene 6 átomos de carbono. Si todos ellos fueran ¹⁴C, el número de átomos radiactivos en un mol de glucosa sería N = 6 x 6.023·10²³, con lo que la actividad específica máxima es
AE = 6 x 6.023·10²³ mol^-1 x 1.04·10^-22 Ci = 376 Ci/mol

Si la queremos por unidad de masa, usamos la masa molecular de la glucosa:
AE = (376 Ci/mol) / (192 g/mol) = 1.96 Ci/g

Problema 21

La actividad del ¹⁴C es: A = N x 1.04·10^-22 Ci (véase la respuesta al anterior).

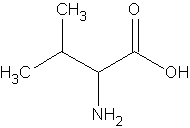La valina tiene 5 átomos de carbono y una masa molecular de 117. Si todos ellos fueran ¹⁴C, el número de átomos radiactivos en un mol de valina sería N = 5 x 6.023·10²³, con lo que la actividad específica máxima es
AE = 5 x 6.023·10²³ mol^-1 x 1.04·10^-22 Ci = 313 Ci/mol

Y por unidad de masa es:
AE = (313 Ci/mol) / (117 g/mol) = 2.67 Ci/g

Problema 22

(Respuesta simplificada; véanse los detalles en las respuestas de 20 y 21).

a) La actividad del ¹⁴C es: A = N x 1.04·10^-22 Ci
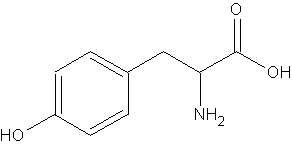
La tirosina tiene 9 átomos de carbono y una masa molecular de 181. La actividad específica máxima será de
AE = 9 x 6.023·10²³ mol^-1 x 1.04·10^-22 Ci = 564 Ci/mol = 0.564 Ci/mmol

b) 250 mCi/mmol / 564 mCi/mmol = 0.443 = 44.3% de los átomos de C serán ¹⁴C.

Problema 23

La actividad (concentración) se diluye en el volumen total de sangre:

A_i x V_i = A_f x V_f
1.77·10⁷ cpm/mL x 2 mL = 1.5·10⁵ cpm/mL x (2mL+V)
V = 234 mL

Problema 24

La actividad del fragmento de DNA será de 1 nCi/mmol por cada residuo de A que contenga, es decir:

AE = 3 nCi/μmol = 3 mCi/mol

Problema 25

(léase la ayuda de arriba)

disolución de partida marcada	disolución de partida fría	agua	disolución final
(1)	(2)	(3)	(4)
V₁ = 1mL AE₁ = 200 Ci/mol A₁ = 50 μCi	V₂ mL C₂ = 5 mM	V₃ mL	V₄ = V₁ + V₂ + V₃ C₄ = 2 mM AE₄ = 5 Ci/mmol

Balance de materia:
C₁ V₁ + C₂ V₂ = C₄ V₄ ; 0.25 mM x 1 mL + 5 mM x V₂ mL = 2 mM x (1 + V₂ + V₃ ) mL

Y balance de actividad:
A₁ + 0 + 0 = A₄ ; 50 μCi = AE₄ x (0.25 μmol + 5 μmol/mL x V₂ mL + 0) ; V₂ = 1.95 mL

Entre ambas: V₃ = 2.05 mL

Respuesta: se debe mezclar la uridina marcada (1 mL) con 1.95 mL de uridina fría y 2.05 mL de agua.

Problema 26

Balance de masa (de Gly):
f x 152.6 mg + 6 mg = m

Balance de radiactividad (de [¹⁴C]Gly):
0 + 120 cpm/mg x 6 mg = 59 cpm/mg x m

( f es la fracción en masa de Gly, o riqueza, con respecto al hidrolizado)
( m es la masa de Gly en la mezcla final)

De la segunda ecuación: m = 720/59 = 12.20 mg
Que, llevado a la primera ecuación, da: f = 6.20/152.6 = 0.0406 = 4.06%

Problema 27

(léase la ayuda de arriba)

Los contenidos (% mol de base/mol de ácido nucleico) de cada hebra serán:

	A	G	C	T
DNA(+)	19%	31%	31%	19%
DNA(-)	19%(*)	31%	31%	19%
				U
RNA(+)	19%	31%	31%	19%(*)

* radiactivo

Como sólo una de las dos hebras está marcada, el DNA de doble hebra tiene un 9.5% de adenosina radiactiva, mientras que el RNA tiene un 19% de citidina radiactiva.

a) Actividad del DNA:
1 mol de dsDNA (double strand DNA, DNA bicatenario) tiene una actividad:
0.095 mol A* x 1 mCi/mol = 0.095 mCi
Luego la actividad específica del dsDNA es de 0.095 mCi/mol

b) Actividad del RNA:
1 mol de RNA tiene una actividad de:
0.31 mol C* x 2·10⁶ cpm/(g CTP) x (100 dpm/50 cpm) x (1 Ci/2.22·10¹² dpm) = 0.559 μCi x (mol C) / (g CTP)
Como la masa molecular del CTP es de 467 (véase la ayuda de arribaμ), su masa molar es 467 g/mol y entonces la actividad es: 0.559 x 467 μCi = 261 μCi
Y la actividad específica del RNA es de 261 μCi/mol = 0.261 mCi/mol

Problema 28

Si el rendimiento fuera del 100% se incorporaría 1 mol de dansilo por mol de polipéptido (o de aminoácido N-terminal); a 100 nmol de proteína, con 2 aminoácidos N-terminales, se incorporarían 200 nmol de dansilo.

Veamos los que se han incorporado realmente:

	1385 cpm			100 dpm
A =	––––––––––	x 2 mL = 27700 cpm	x	–––––––––––	= 34625 dpm
	0.1 mL			80 cpm

que, teniendo en cuenta la actividad específica del dansilo, corresponden a:

34625 dpm		1 Ci
–––––––––––	x	––––––––––––––	= 1.56·10^-7 mol de dansilo incorporado
0.1 Ci/mol		2.22·10¹² dpm

Por tanto, el rendimiento de la dansilación es de

1.56·10^-7 mol
–––––––––––	= 0.78 = 78%
200·10^-9 mol

Problema 29

El péptido 1, que es el deseado (Gly-Val-Pro-Ala), tendrá una actividad de 10⁴ cpm/mmol

El péptido 2, al tener dos residuos de Gly, tendrá una actividad de 2·10⁴ cpm/mmol

La actividad específica de la mezcla será:
AE = 0.90 x 10⁴ cpm/mmol + 0.10 x 2·10⁴ cpm/mmol = 1.1·10⁴ cpm/mmol

Para pasar a μCi/g, teniendo en cuenta que 1 mol de cualquiera de los péptidos tiene 4 moles de aminoácidos, pesará 4 x 110 gramos y:

	100 dpm		1 Ci		10³ mmol		1 mol
AE = 1.1·10⁴ cpm/mmol x	–––––––––	x	–––––––––––––––	x	–––––––––––	x	–––––––
	80 cpm		2.22·10¹² dpm		mol		440 g

AE = 1.41·10^-8 Ci/g

Problema 30

a) Para ¹³¹I:

	ln2		ln2
λ =	––––	=	––––––	= 0.0856 d^-1
	t_1/2		8.1 d

	–dN
1 dpm = 1 min^-1 = A =	––––	= λ N = 0.0856 d^-1 x N
	dt

de donde

	1 min^-1		24 h		60 min
N =	–––––––––––	x	–––––	x	–––––––	= 16800 (átomos)
	0.0856 d^-1		1 d		1 h

b) Similarmente para ³²P: N = 29700 átomos
(una vida media más larga significa una menor radiactividad para el mismo nº de átomos, por eso para conseguir la misma actividad hace falta mayor cantidad de P).

Problema 31

"yodoacetato-¹⁴C" debe escribirse correctamente como yodo[¹⁴C]acetato

La reacción es Cys + 2 IAcO^-

a)

En 1 nmol proteína hay 5 nmol Cys, se necesitan 10 nmol de yodoacetato
10 nmol / 1 nCi/nmol = 10 nCi son necesarios = 0.01 μCi

b)

	1 mCi		5 mol Cys
AE_prot. =	–––––––––––	x	––––––––––	= 5 mCi/mmol prot. = 5 Ci/mol
	mmol Cys		mol prot.