1.
La disolución "A" tiene una concentración 2 mM. La disolución "B" tiene una concentración 2 µM.
a) ¿Cuántas veces más concentrada es A que B?
b) ¿Cuál es el factor de dilución para preparar B a partir de A?
El factor de dilución es 1000, o el proceso A -> B es una dilución 1/1000
2.
¿Cómo prepararías medio litro de disolución 100 mM de sacarosa si dispones de una disolución 1 M?
1 M / 100 mM = 1000 mM / 100 mM = 10
Por lo tanto, se requiere diluir 10 veces (dicho de otro modo, hacer una dilución 1/10). Es decir, 1/10 de la disolución final estará formada por líquido de la inicial.
1/10 × medio litro = 1/10 × 500 mL = 50 mL
que se deberá tomar de la disolución de partida. El resto (500 mL - 50 mL = 450 mL) será agua.
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
V1 es la incógnita
Las otras variables son conocidas:
c1 = 1 M = 1000 mMV1 = (c2V2) / c1
c2 = 100 mM
V2 = medio litro = 500 mL
V1 = (100 mM × 500 mL) / 1000 mM
simplificando 100 / 1000 , y mM arriba y abajo:
V1 = (1 × 500 mL) / 10
V1 = 50 mL
3.
¿Cómo prepararías 200 mL de disolución 200 mM de NaCl si dispones de una disolución 5 M?
5 M / 200 mM = 5000 mM / 200 mM = 25
Por lo tanto, se requiere diluir 25 veces (dicho de otro modo, hacer una dilución 1/25). Es decir, 1/25 de la disolución final estará formada por líquido de la inicial.
1/25 × 200 mL = 8 mL
que se deberá tomar de la disolución de partida. El resto (200 mL - 8 mL = 192 mL) será agua.
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
V1 es la incógnita
Las otras variables son conocidas:
c1 = 5 M = 5000 mMV1 = (c2V2) / c1
c2 = 200 mM
V2 = 200 mL
V1 = (200 mM × 200 mL) / 5000 mM
simplificando tres ceros y mM arriba y abajo:
V1 = (2 × 20 mL) / 5
V1 = 40 / 5 mL = 8 mL
4.
Necesitas preparar una disolución 10 mM de NaOH. Dispones de una 1 M. ¿Cuál es el factor de dilución?
Otra forma de pensar en la pregunta: ¿cuántas veces más concentrada es la disolución inicial que la final?
Factor de dilución = 1 M / 10 mM = 1000 mM / 10 mM = 100
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
Reordena la ecuación para mostrar la relación entre las dos concentraciones. Esta relación (expresada como cociente o razón) es el factor de dilución:
c1 / c2 = V2 / V1 = F.D.
1 M / 10 mM = 1000 mM / 10 mM = 100 (es decir, hay que diluir 100 veces)
5.
Necesitas preparar una disolución 100 mM de Tris base. Dispones de una 1 M. ¿Qué proporción (fracción) de la disolución final estará formada por la inicial?
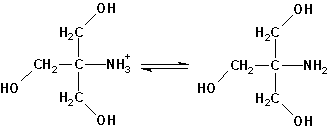
A la forma básica se la llama Tris base, a la ácida Tris hidrocloruro. Lo más frecuente al preparar tampones es usar la forma básica y ajustar el pH deseado añadiendo una disolución de HCl, por eso se habla de tampones Tris-HCl.
La proporción de disolución final que estará formada por la inicial es el cociente de volúmenes, que es el cociente (inverso) de concentraciones. Dicho de otro modo, el volumen aumenta por el mismo factor que disminuye la concentración.
1 M / 100 mM = 1000 mM / 100 mM = 10
Este es el factor de dilución. Usa su inverso para averiguar la proporción de volumen:
1/10 = 0.1 = 10% del volumen final será disolución inicial. El resto será agua.
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
Reordena la ecuación para mostrar la relación entre las dos concentraciones. Esta relación (expresada como cociente o razón) es el factor de dilución:
c1 / c2 = V2 / V1 = F.D.
1 M / 100 mM = 1000 mM / 100 mM = 10
Nota: podemos pensar en el factor de dilución así o al contrario, como cociente entre volumen inicial y final (el inverso del mostrado). Ambas formas de expresarlo son válidas: "el factor de dilución es 10" o "el factor de dilución es 1/10". Sabemos que siempre la disolución final tendrá una concentración menor, y un volumen mayor, que la inicial. No hay confusión posible.
6.
a) Un procedimiento requiere la preparación de diluciones 1/10 sucesivas de la muestra (tambén llamadas diluciones seriadas). Si quieres muestras de 1 mL, ¿cómo procederás para preparar la serie de diluciones?
Debes, por tanto, calcular el volumen que hay que tomar de cada muestra (dilución i) para preparar la siguiente (dilución i+1).
Factor de dilución = 10 (dilución 1/10)
Usa el inverso del factor de dilución: 1/10 de cada disolución estará formado por la anterior.
(1/10) × 1.0 mL = 0.1 mL = 100 µL
Es decir, cada dilución se prepara mezclando 100 µL de la anterior con 900 µL de agua.
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
Buscamos V1, pero no conocemos c1 ni c2.
Despeja V1 en
la ecuación:
V1 = (c2 / c1) × V2
De este modo, se usa directamente el cociente de concentraciones (c2
/ c1) —que es una forma de expresar el factor de dilución—.
Puesto que la concentración siempre irá disminuyendo,
no hay ambigüedad: c2 / c1 = 1/10, no 10.
Sustituyendo:
V1 = 1/10 × 1.0 mL = 0.1 mL = 100 µL
Es decir, cada dilución se prepara mezclando 100 µL de la anterior con 900 µL de agua.
b) ¿Cuál será la concentración relativa tras cuatro de tales diluciones?
1/10 × 1/10 × 1/10 × 1/10 = 1/10000 = 1/104 = 10−4
o bien
(10−1)4 = 10−4
Es decir, la concentración tras la cuarta dilución es 10−4 veces la de partida.
7.
Tienes una disolución de proteínas y, tras realizar un ensayo de medida de concentración, te das cuenta de que la tendrás que diluir para obtener una lectura de absorbancia fiable. Diluyes la muestra 1:1 tres veces sucesivas y cada una de ellas sigue estando demasiado concentrada. Por último, desesperado, diluyes 1/10 la última muestra que has preparado y por fin la puedes medir. El resultado es 100 µg/mL. ¿Cuál es la concentración de la muestra original?
Otros ejemplos:
1:2 = 1/3
1:5 = 1/6
3:7 = 3/10
1:5:4 = una parte de A, 5 partes de B y 4 partes
de C (esto no se llamará habitualmente una dilución,
sino una mezcla, aunque cada componente se diluye al hacerla).
Para evitar confusiones, procura utilizar siempre la notación con barra de dividir, y no los dos puntos. Alguien podría entender que 1:3 es un factor de dilución 3, cuando tú quieres indicar un factor 4. (La única situación imposible de confundir es la 1:1)
| Factor | Factor global | |
| Primera dilución 1:1 | 2 | 2 |
| Segunda dilución 1:1 | 2 | 2×2 = 4 |
| Tercera dilución 1:1 | 2 | 4×2 = 8 |
| Dilución 1/10 | 10 | 8×10 = 80 |
Por lo tanto, la muestra final está 80 veces menos concentrada
que la original.
La concentración de partida será:
80 × 100 µg/mL = 8000 µg/mL = 8 mg/mL
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
Lo aplicamos a cada dilución sucesivamente:
| la dilución nos dice | resultado | ||
| Primera dilución 1:1 | V2 / V1= 2 | c1V1 = c2V2 | c1 = 2×c2 |
| Segunda dilución 1:1 | V3 / V2= 2 | c2V2 = c3V3 | c2 = 2×c3 |
| Tercera dilución 1:1 | V4 / V3= 2 | c3V3 = c4V4 | c3 = 2×c4 |
| Dilución 1/10 | V5 / V4= 10 | c4V4 = c5V5 | c4 = 10×c5 |
| globalmente: | c1 = 80×c5 | ||
Luego, si la concentración final (c5) es de 100 µg/mL,
la inicial (c5) sería de
80 × 100 µg/mL = 8000 µg/mL = 8 mg/mL
8.
Calcula el factor de dilución sufrido al completar el proceso siguiente:
Se añaden 0.5 mL de la disolución de partida a 1.5 mL de diluyente. De la disolución resultante, se toman 0.7 mL y se mezclan con 1.4 mL de diluyente. Finalmente, 1.0 mL de esta disolución se añaden a 19.0 mL de diluyente.
| Factor | Factor global | ||
| Primera dilución | 0.5 / 2 | 4 | 4 |
| Segunda dilución | 0.7 / 2.1 | 3 | 4×3 = 12 |
| Tercera dilución | 1 / 20 | 20 | 12×20 = 240 |
Por lo tanto, el factor de dilución es 240; la muestra final está 240 veces menos concentrada que la original; la dilución global es 1/240.
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = cuánto se quiere preparar |
Lo aplicamos a cada dilución sucesivamente:
| resultado | |||
| Primera dilución | c1V1 = c2V2 | c1 × 0.5 = c2 × (0.5+1.5) | c1 / c2 = (0.5+1.5)/0.5 |
| Segunda dilución | c2V2 = c3V3 | c2 × 0.7 = c3 × (0.7+1.4) | c2 / c3 = (0.7+1.4)/0.7 |
| Tercera dilución | c3V3 = c4V4 | c3 × 1.0 = c4 × (1+19) | c3 / c4 = (1+19)/1 |
c1/c4 = c1/c2 × c2/c3 × c3/c4 = (2/0.5) × (2.1/0.7) × (20/1) = 4×3×20 = 240
Por lo tanto, el factor de dilución es 240; la muestra final está 240 veces menos concentrada que la original; la dilución global es 1/240
9.
Se prepara una disolución mezclando 2.0 mL de glucosa 15 mM con 3.0 mL de NaCl 0.5 M.
¿Cuáles son las concentraciones de ambos componentes en la disolución?
NaCl: pasa de estar disuelto en 3 mL a estarlo en 2+3=5 mL. Por tanto, el factor de dilución es 3/5, y la concentración final será de 0.5 M × (3 / 5) = 0.3 M
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = volumen total |
Glucosa: 15 mM × 2mL = c2 ×
(2+3) mL ![]() c2 = (30 / 5) mM = 6 mM
c2 = (30 / 5) mM = 6 mM
NaCl: 0.5 M × 3mL = c2 ×
(2+3) mL ![]() c2 = (0.5 × 3 / 5) M = 0.3
M
c2 = (0.5 × 3 / 5) M = 0.3
M
10.
Se prepara una disolución mezclando 1.0 mL de sacarosa 250 mM con 4.0 mL de NaCl 1.0 M.
¿Cuáles son las concentraciones de ambos componentes en la disolución?
NaCl: pasa de estar disuelto en 4 mL a estarlo en 1+4=5 mL. Por tanto, el factor de dilución es 4/5, y la concentración final será de 1 M × (4 / 5) = 0.8 M
|
c1V1 = c2V2
la situación (1) es antes de la dilución (disolución
de partida),
la situación (2) es tras la dilución (disolución final). |
V1 = cuánta disolución de partida hay que
añadir
c1 = concentración de la de partida c2 = concentración de la final V2 = volumen total |
Sacarosa: 250 mM × 1 mL = c2 ×
(1+4) mL ![]() c2 = (250 / 5) mM = 50 mM
c2 = (250 / 5) mM = 50 mM
NaCl: 1 M × 4 mL = c2 ×
(1+4) mL ![]() c2 = (1 × 4 / 5) M = 0.8
M
c2 = (1 × 4 / 5) M = 0.8
M